An astronomical object is usually a celestial entity associated with some natural phenomenon. In DISHAS, astronomical objects are used as a way to classify astronomical tables into broader categories.
DISHAS implement different calendars used by historical actors. The calendars define the time units used in the expression of the arguments of mean motion tables. These calendars vary mainly according to:
- the length of their years,
- their ways to define intercalation rules for leap years,
- the length, order, and names of their month in ordinary and leap years
- their era and convention for beginning of the astronomical days
The era is the starting date of a calendar expressed in Julian Day Number.
Tables for days are a type of mean motion table where “day” is used as the time unit for the argument. The entries provide motion for a given number (and not position).
Refers to either the partial or total occultation of the Sun behind the Moon (solar eclipse), or the partial or total dipping of the Moon into the shadow of the Earth (lunar eclipse). A given solar eclipse appears differently and at different moments in different places of the Earth, while a lunar eclipse is seen simultaneously by all observers. The precondition for any eclipse is that Sun and Moon are either in conjunction (at the same place on the ecliptic circle) or in opposition (at opposite places on the ecliptic circle).
Imaginary sphere carrying all the constellations of the fixed stars, observed to move with respect to the referential of the ecliptic circle, in particular to the position of the Sun at the equinoxes.
Epoch is one of the three localisation parameters that can be attached to mean motion tables (see also Root and Place). The epoch of a mean motion table is the actual date from which the collected year table starts (as opposed to the era of the calendar on which the table is based). It is thus usually the first argument of the collected year table but can be also defined with more accuracy if the historical source allows. The epoch is expressed by the user according to the calendar system associated with the table. The system will convert this expression also as a Julian Day Number.
Formula definitions are modern mathematical expressions of historical theoretical models, usually geometrically expressed, on which the different types of astronomical tables are based. They rely on a given set of (implicit) parameters depending on the table type. A given table type can have more than one “Formula definition” because historical actors have considered different theoretical models for the same type of astronomical table. “Formula definition” is used in two main ways in DISHAS. First they might provide suggestions for the table values and thus help in the table input. Second they are essential tools to squeeze implicit parameters out of the table content.
Historical actors are individuals or groups related to the items or stored in the database. They include authors, copyists, owners, dedicatees, etc. associated with the materials containing the . Within the frame and scope of our database, we collect certain information related to the historical actors, namely, their names, the periods in which they flourished (floruit), and the places where they lived. This enables us to create a standardized lists of actors. With the additional (and highly recommended) Virtual International Authority File (VIAF) number recorded, the database makes it possible to align names added at a later stage with a larger, normalized, authority register of person names. We collect information about the actors in order to build prosopographic data.
An intellectual author is a contemporary historian who has produced an edition that is stored in the database. This historian could be different from the person entering the data into the database. For example, in certain instances, a scholar (user) may be entering the data from an edition created by another historian (from, perhaps, an unpublished collection). The intellectual author in this case is the creator-historian and not the scholar (user). Collecting information about intellectual authors validates the factual reliability of the database. This effort helps preserve the of previous generations of historians as a way to foster and encourage further studies. The information collected about intellectual authors helps identify the modern scholarship of the edition entered in the database.
Tables for hours are a type of mean motion table where “hour” is used as the time unit for the argument. The entries provide motion for a given number (and not position).
Tables for hours are a type of mean motion table where “hour” is used as the time unit for the argument. The entries provide motion for a given number (and not position).
In academic publishing, a scientific journal is a periodical publication intended to further the progress of science, usually by reporting new research.
Second brightest planet returning close to the same place among the fixed stars with a period of about 12 years.
For our purposes, a library is the current location where a is situated. The knowledge of the physical location of the library where the is held is important for establishing the reliability of the database as a resource for research. Facilitated with assistance tools like ISNI, it is possible to enter institutional information into the database that is helpful for registering and identifying the correct library. For other libraries (not in the ISNI records), new entries will help create records of their existence in the database for subsequent use.
There are three types of localisation parameters that can be associated to mean motion table when they give position: Epoch, Place and Root. The time localisation is called the Epoch. The longitude for which the table is computed is called the Place. The celestial position of the object for this time and place is called the Root.
Although they can occasionally be defined with more accuracy when the historical source allows, they are conveniently defined with respect to the first argument and entries of tables for collected years:
| Date | Place of the Sun for Paris |
|---|
| 2019 | 11s03;52 |
| 2039 | 11s03;49 |
| 2059 | 11s03;47 |
| ... | ... |
Its reddish glow varies in brightness reaching a peak about every two years: in this situation the planet also makes a westward loop and is close to a position opposite the Sun on the heavenly sphere.
There are two kinds of mathematical parameters.
A table is said to be ‘displaced’ when a constant value is added to its arguments and/or its entry. The value of these added constants is the first kind of mathematical parameters.
A table can also be ‘shifted’. This happens when the ordering of the arguments and/or entry is modified according to a permutation cycle. The number of shifts in the permutation cycle is the second type of mathematical parameter.
The main purpose of identifying mathematical parameters is to compare displaced and/or shifted tables with those which are not displaced or shifted. We note that both shifted and/or displaced tables may rely on the same set of astronomical parameters. Different sources can share the same mathematical parameters. Additionally, shifts and displacements are peculiar kinds of mathematical techniques linked to the manipulation of table sets and as such are worthy of investigation in their own right.
Base example
|
Argument
|
Entry
|
|
10
|
7
|
|
20
|
8
|
|
30
|
9
|
|
40
|
10
|
Shift
Argument-shift and entry-shift are always integer numbers
Argument-Shift = 2
Entry-Shift = 0
|
Argument
|
Entry
|
|
30
|
7
|
|
40
|
8
|
|
10
|
9
|
|
20
|
10
|
Argument-Shift = 0
Entry-Shift = 2
|
Argument
|
Entry
|
|
10
|
9
|
|
20
|
10
|
|
30
|
7
|
|
40
|
8
|
Argument-Shift = 2
Entry-Shift = 3
|
Argument
|
Entry
|
|
30
|
10
|
|
40
|
7
|
|
10
|
8
|
|
20
|
9
|
Displacement
Argument-displacement and entry-displacement are the same type of numbers as the value of the table. It might vary from argument and entry.
Argument-Displacement = 2
Entry-Displacement = 0
|
Argument
|
Entry
|
|
12
|
7
|
|
22
|
8
|
|
32
|
9
|
|
42
|
10
|
Argument-Displacement = 0
Entry-Displacement = 3
|
Argument
|
Entry
|
|
10
|
10
|
|
20
|
11
|
|
30
|
12
|
|
40
|
13
|
Argument-Displacement = 2
Entry-Shift = 3
|
Argument
|
Entry
|
|
12
|
10
|
|
22
|
7
|
|
32
|
8
|
|
42
|
9
|
Mean motion tables are at the root of astronomical computation in most mathematical astronomy traditions. They provide a first approximation of the position of a celestial object at a given moment assuming that the object motion is at constant velocity. The arguments are of a temporal nature (duration or date), the entry of positional nature (an arc providing a position or motion), which result in combinations such as motion per duration or position per date.
Because the entries of some mean motion tables give the position of celestial objects they carry time and space localization information: more precisely they are valid at a given longitude. These information are captured in localisation parameters: the epoch, the root, and the place parameters
Because the arguments of the mean motion table are of temporal nature, their expression depends on a specific calendar system. The edition of mean motion tables will thus be presented as a collection of different types of tables where the arguments will typically be years, months, days, hours and minutes. DISHAS allows us to manage the most common calendrical systems used by historical actors. Argument of mean motion table commonly expresses elapsed time (e.g. 2 years means that two years are elapsed). This convention is named “complete”. The opposite convention is named “incomplete” (e.g. when 2 years mean one year elapsed and currently in the second year).
Quickly changing its position with respect to the Sun, it comes back against the same star in a cycle of about 88 days, appearing sometimes east and sometimes west but Mercury is difficult to observe because of its proximity to the Sun.
Months tables are a type of mean motion tables where “months” are used as the time unit for the arguments. The exact length, names and orders of the months depends on the calendrical systems. In particular it will be important for the users to define if the year considered is leap or ordinary. It will be also important for the user to define what is the first month of the table (which can be different from the first month of the year in the calendar system). The entries provide motion (and not position).
Months are a type of calendrical unit, dividing the year usually according to cycles linked with the moon. There is a great variety of months lengths, names, and orders in historical calendars. Depending on the nature of the years (ordinary or leap) some months can have a shorter (ordinary) or a longer length (leap). In some calendar systems leap years can also have a supplementary (intercalary) month.
The object in the sky moving fastest with respect to the fixed stars (about 13° per day), and its disk appearing fully or only partially depending on its position with respect to the Sun.
Historical actors have used various units to express time and space relations in the astral sciences. Some of these units are directly related to celestial objects, others to measuring instruments. Some units are mathematical and abstract. Often, these units are distinct from the measurements of degrees and seconds, which are in common use today. Thus, modern units are not a suitable tool to record historical astronomical tables in most cases. The common units used by historical actors in the astral sciences are implemented in the database for historical accuracy. This will also allow for mathematical analysis in DISHAS.
is a group of astronomical quantities that describes tables at the level of astronomical theory. can be shared by several tables across different traditions.
Broadly speaking, there are two kinds of parameters: explicit parameters that are directly read off the table (e.g., the maximum value(s)); and implicit parameters that need to be retrieved from the computationally (e.g, solar eccentricity). In some cases, these explicit or implicit parameters are only significant in groups. In other instances, however, parameters can be independently significant.
Parameters are a central tool in (i) delineating and connecting astronomical traditions and (ii) analyzing the mathematical and astronomical content of the tables.
is only linked to an intellectual author through because a single can be shared by many different sources.
Parameters are astronomical quantities that describes tables at the level of astronomical theory. Broadly speaking, there are two kinds of parameters: explicit parameters that are directly read off the table (e.g., the maximum value(s)); and implicit parameters that need to be retrieved from the computationally (e.g, solar eccentricity). Implicit parameters are often elements of modern functional expressions allowing the user to recompute the tables with which they are associated.
Parameters are the fundamental building block of which describe different table types. They are meant to compare sources from different traditions, which possibly used different units of measure. In order to allow comparison across these traditions, it is necessary to standardize units to express parameters. The astronomical parameters are linked to the (and not to the original text) because a given is always attributed to a table by an intellectual author after analysis.
The definition of a place depends on the object related to it. For , it refers to the place of production. For an author, it refers to his main place of activity where his can be (approximately or precisely) geo-localised. For , the place refers to the original place of conception. This information is important for understanding the diffusion and circulation of items in various and traditions.
Collecting information about the place, including, in some instances, its latitude and longitude, helps us locate objects on a map. This visual representation can become an important tool for textual analysis and circulation studies.
Place (longitude) is also one of the three localisation parameters that can be attached to a mean motion table.
Place is one of the three localisation parameters that can be attached to a mean motion table (see also Root and Epoch). It is the geographical longitude for which the positional entries of the mean motion table are calculated. We express this information using conventions of the historical actors. We specify the place name and its longitude relatively to a base meridian. Conversion into modern longitude are not yet available in DISHAS
A is a manuscript or an early printed edition in which the is found, usually as part of . It is essential for the reliability of DISHAS that it provides accurate identification of its . Additionally, having accurate information about in the database can prove to be an important tool to study the history of modern collections in the astral sciences. Information about these helps us identify the physical institution or library that holds them. This identification allows scholars to locate the original source for further investigation.
Root is one of the three localisation parameters that can be attached to mean motion tables (see also Epoch and Place). It is the position attached to the Epoch parameter. It is thus usually the first entry of the collected year table but can be also defined with accuracy if the historical source allows.
Changing its position only very slowly and returning close to the same constellations of fixed stars in about 30 years.
A secondary source is a book, an article, a chapter, etc. that indicates a contemporary edition, or a survey of the table. Every edited document in the database is only linked to a single secondary source for the sake of brevity. Information about secondary sources provides a reliable and tractable resource for further studies. This information will help current and future scholars use the database for their research. Secondary sources provide reference material for further studies and, as such, the information collected about it is aimed to make the database competent in facilitating this.
Study of astronomical phenomena related to the daily motion of the celestial sphere, in particular as they are seen from different points of observation on earth.
The most brilliant of the objects in the sky, appears to change its place with respect to the fixed stars about 1° per day.
The is the collection of numerical values in the . The relation between these numerical values and those, which are attested in the (s) associated with the , depends on the type of edition selected. We understand to be the type of done by the intellectual author responsible for its creation.
Comparing numerical contents of various tables and building new computational and analytic tools are both central to the aim of DISHAS. In order to achieve these aims, a minimum level of standardization in the layout of tables and the format of recorded numbers is necessary. However, it is equally important to allow a certain amount of flexibility to reflect the practices of historical actors faithfully. Hence, there are several possibilities about table layout, symmetries, table types, and types of numbers.
The choices of an intellectual author are carefully documented to ensure a meaningful comparison between the of various . We collect information about the for display purposes.
is a production credited to a contemporary intellectual author or historian. It documents one specific table, text or diagram. This document can be from a previously edited source or a new edition created using the web interface of DISHAS. With respect to astronomical tables, can have various edition types, including an edition of a specific original text, a recomputation, or a new production based on multiple sources.
An essential goal of the database is to make editions of astronomical tables that are accessible and comparable. In achieving this, , as classified in various edition types, help (i) identify mathematical and astronomical parameters, (ii) examine and develop critical and computational tools for creating new editions, and (iii) provide a centralized resource for studying astronomical tables from different traditions.
We collect general information about the edition (e.g., the title, the date of creation, etc.) so to record the metadata associated with it. This, along with the other information associated with the , helps us unify and create standards for comparison in our database.
We collect secondary source information for bibliographic accuracy and catalogue reference.
Three types of edition are defined in DISHAS.
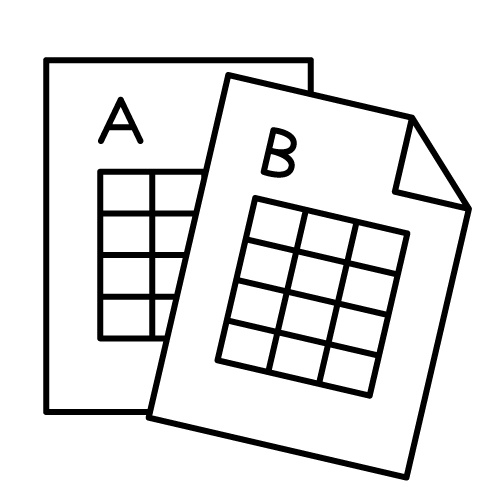
- Type-A Editions are numerically consistent tables, which are essentially dependent on one manuscript source.
- Type-B Editions are critical editions that will typically depend on more than one manuscript source.
- Type-C Editions are numerically recomputed tables that depend on a mathematical model reconstructed by the editor, and which are not necessarily linked to any specific manuscript sources.
Tables are classified according to different types. These different types correspond to the specific steps in astronomical computations organized by historical actors. In modern terms, these types correspond to distinct classes of mathematical functions which express a portion of an underlying astronomical theory.
is a table, text, or diagram as it appears in a given . In instances where the actual state of the item is the result of several distinctive production acts (e.g., an extra column added to a table by a later actor), each distinct stage of production is considered to be a specific item. A scholar (user) may input these instances as separate . The , as it appears in the , is the fundamental unit of the database. Hence, elementary units are individual tables, diagrams, or texts that are actually witnessed in specific . This level of granularity is central to make DISHAS an efficient tool for mathematical analysis and critical editing. We collect material information about the to allow source criticism. These include the date and the place of production, the title of the , the manuscript shelfmark, etc.
In the current stage of development of DISHAS, only tables are considered; texts and diagram will be included at a later stage.
Primarily a set of mathematical quantities used to analyse relations between arcs and chords in a circle, it is progressively shaped as tools to resolve triangles.
Three types of edition are defined in DISHAS.
- The Type-A Edition is a numerically consistent table depending on a single . It involves rendering the individual table (taken from individual MSS of the same ) from its diplomatic transcription into a more numericallyconsistent format, i.e., a format free of any data integrity errors. The following is a list, albeit not an exhaustive one, of the different types of strategies employed in creating a numerically consistent table.
- Numerical parsing on a local and global scale to ensure regularity (e.g., correcting a number to maintain simple mathematical regularity). It should be noted here that this inspection is merely observational and not computational.
- Using pattern recognition and visual inspection to correct numbers for constancy, uniformity, and accuracy (in reproduction).
- Noting all numerical changes (e.g., instances where ambiguous, dubious, or inconsistent numbers are altered, alternatives or originals are duly noted as comments).
- The Type-B Edition is a critical edition. It involves employing the different individual tables (belonging to the same , but taken from different MSS) and forming an critical edition table. This process can be defined based on a few different strategies:
- Any eclectic, stemmatic, or copy-text method (in general, any philological method) of comparing the different 'witness' tables (from Type A) and establishing a critical 'base' numerical table, with all variants duly noted in comments. These comments effectively make the critical apparatus.
- Any mathematical method (from type C) of establishing a critical 'base' numerical table and then employing tables (from type A) to note the variants.
- Any combination of the two strategies above.
- Additionally, any previously 'critically' edited table (from a set of extant or non-existing manuscripts) belonging to the same table-type and (as set in type A) can also be stored in type B here. In such cases, it is important to note any relation, if applicable, of this previous to the different tables in type A. Failing this, a common reference to the and table type becomes minimally necessary.
Several different 'critical editions' (based on different editorial strategies) of the same table may be stored in this stage; all of which, are identified with the correct relational structure to the tables of types A and C. - The Type-C Edition consists of numerically recomputed tables. These tables are generated by a modern scholar based on his or her own understanding of the mathematical apparatus presumably intended to have been used by the original author in his time. These tables form a collection of our modern efforts to reconstruct numerical tables within its historical context. These tables are generated based on the following possible strategies:
- A modern mathematical recomputation of the table based on (a) choice of the appropriate parameter, (b) mathematical equations governing the underlying function tabulated, or (c) selection of a suitable generative or iterative algorithm.
- Any other derivatives or combinations of such mathematical procedures, algorithms, iterative techniques, rounding schemes, etc. as can be used to generate the numerical entries of the table from separate mathematical tables that are also stored in DISHAS.
Over the course of time and in different domains of the astral sciences, historical actors have used different types of numbers both to make their computations and to shape their tables. Some are fully sexagesimal, others partially so, while still others rely on floating numbers, to name just a few variations. These different types of numbers are often very distinct from the decimal systems used in modern numerical programming. As a consequence, modern decimals are not always a suitable tool to record historical astronomical tables.
The common types of numbers used by historical actors in astral sciences are implemented in the database for historical accuracy and computational analysis. This level of complexity combines with a similar one concerning units.
DISHAS uses six types of number
- Sexagesimal
- Floating sexagesimal: floating sexagesimal numbers are numbers with no order of magnitude and with a factor 60 from one position to the next.
- Historical: revolution and sign.
- Integer and sexagesimal: integer and sexagesimal are numbers with an integer part expressed in the decimal system and a fractional part expressed in a sexagesimal system.
- Historical decimal: in Chinese sources,fractionalparts can be expressed with 'fen' and 'miao'. There are100 'fen' in the unit and 100 'miao' in a 'fen'. Thus, formally speaking, historical decimals are three-position numbers with a factor 100 between each position. 6. Temporal: present the duration of time converted into days following sexagesimal notation. Ex : 7d6;30,05.
The brightest of the planets, visible alternately as evening or morning star, each time for about 9 months, and disappearing in between in the glow of the Sun.
An astronomical - inspired by the FRBR definition of entity - is a distinct intellectual creation consisting of tables, texts, or diagrams. A needs to be identified by a current title or incipit. When possible supplementary information like place, date, author or translator is very useful for studying the circulation of the . Its content and organisation may vary depending on the particular .
In DISHAS, are defined "bottom-up" from the attached to them in different manuscripts rather than the over way around. We can analyse the different attestations of a given as , which are the fundamental units of DISHAS. For instance, one can identify a core set of tables around which various satellite tables, texts, or diagrams may be presented depending on the . With this design, the geographical and chronological evolution of these dynamical sets of can be analyzed and studied. This ability is essential when it comes to critically editing . Additionally, the choice of as the fundamental unit also allows the user to analyse the intellectual composition of a given manuscript. This is an important step toward understanding how the medium of the manuscript shaped intellectual traditions.
Years are the longest time unit used in calendar systems. Their exact length depends on the calendar system. Lunar years are usually around 354 days, while solar years are around 365 days. Most calendar systems rely on a distinction between ordinary and leap years. The ordinary years are short, while leap years are longer (with one additional day or month). Leap years are intercalated into ordinary years in different cycles according to the calendars. These systems are usually designed to adjust calendars to the motions of the sun and moon which can not be expressed precisely using integer numbers of days. Years are further divided in month.
Extended years are a type of mean motion table using “year” as the unit of their argument. The exact length of “year” depends on the calendar systems. Their arguments consist of successive years, hence involving leap years and having two distinct tabular differences. This table usually runs up to the number of years in the groups tabulated in the single or collected years. The entries of single years table provide mean motions (and not position).
Collected years are a type of mean motion table using “year” as the unit of their argument. The exact length of “year” depends on the calendar system. They are positional tables: their arguments are dates (and not durations), their entries position (and not motions). As such they are linked to positional parameters (see root, epoch and place). Although the most common case is that the increment of tables for collected years are groups of years, each with the same number of days (e.g. 28 Julian years or Byzantine years, 30 Islamic years), tables in which the mean positions are given for every year also exist.
Single years are a type of mean motion table using “year” as the unit of their argument. The exact length of “year” depends on the calendar system. Their argument consists of groups of years each with the same number of days. They may have different increments (e.g. 20,40,60, 80,100, 200,300,400, 500,..,1000,2000,3000). The entries of single years table provide mean motions (and not positions).